(1a)o en su forma implícita:
(1b)
Ejemplos de ecuaciones diferenciales
Si mediante operaciones algebraicas es posible expresar la ecuación diferencial en la siguiente forma:
(2a)se dirá que es una ecuación diferencial de variables separables. De este modo, en cada miembro de la ecuación se tendrá una única variable. Para resolver este tipo de ecuaciones basta con integrar en cada miembro:
(2b)Ecuaciones homogéneas
Una ecuación de la forma
es homogénea siempre que la función f no dependa de x y y aisladamente, sino únicamente de sus razones y/x o bien x/y. Así pues las ecuaciones homogéneas adoptan la forma
- dy/dx = f(x,y)
Se dice que una ecuación es homogénea si la función f(x, y) es fraccionaria y además el grado de los polinomios de numerador y denominador son los mismos. Por ejemplo:
- dy/dx = F(y/x)1 .
sería homogénea ya que todos los términos de ambos polinomios son de grado 3. Así se procede dividiendo tanto numerador como denominador poro
en función de qué cambio haga más simple su resolución. Llegados a este caso según la elección se puede optar por uno de los dos cambios análogos, que son:
Así se simplifica enormemente y suele quedar separable. Para finalizar solo resta deshacer el cambio, sustituyendo las u(x,y) por su valor como función que se ha establecido.o bien
El caso anterior puede generalizarse a una ecuación diferencial de primer orden de la forma:
(3a)introduciendo la variable u = y/x; la solución de la anterior ecuación viene dada por:
(3b)Ecuaciones lineales de primer orden
La ecuación diferencial lineal de primer orden tiene la forma:
(4a)Y la solución de la misma viene dada por:
(4b)En el caso particulary
, la solución es:
(4c)Ecuación diferencial de Bernoulli
Una ecuación de Bernoulli es aquélla que tiene la forma:
(5a)Donde P(x) y Q(x) son funciones continuas cualesquiera. Su solución para α > 1 viene dada por:
(5b)Dicha solución directa puede obtenerse aplicando paso a paso el siguiente método:
- 1) Cambiar la variable dependiente y por una nueva variable v de la siguiente manera:
- 2) Se diferencia v en función de x.
- 3) Se despeja el diferencial dy del paso anterior y se substituye en la ecuación diferencial original (resultando una ecuación lineal).
- 4) Se encuentra por integración directa la función v en la ecuación:
- donde:
- 5) Se revierte el cambio de variable desde v a y y se encuentra la solución general, en función de su variable original x.
Tipos de ED y Soluciones
Dependiendo del número de variables independientes respecto de las que se deriva, las ecuaciones diferenciales se dividen en:
- Ecuaciones diferenciales ordinarias: aquellas que contienen derivadas respecto a una sola variable independiente.
- Ecuaciones en derivadas parciales: aquellas que contienen derivadas respecto a dos o más variables.
Orden de la ecuación
El orden de la derivada más alta en una ecuación diferencial se llama orden de la ecuación.

Solución de una ecuación diferencial
Tipos de soluciones
Una
solución de una ecuación diferencial es una función que al remplazar a
la función incógnita, en cada caso con las derivaciones
correspondientes, verifica la ecuación, es decir la convierte en una
identidad. Hay tres tipos de soluciones:
- Solución general: una solución de tipo genérico, expresada con una o más constantes. La solución general es un haz de curvas. Tiene un orden de infinitud de acuerdo a su cantidad de constantes (una constante corresponde a una familia simplemente infinita, dos constantes a una familia doblemente infinita, etc). En caso de que la ecuación sea lineal, la solución general se logra como combinación lineal de las soluciones (tantas como el orden de la ecuación) de la ecuación homogénea (que resulta de hacer el término no dependiente de y(x) ni de sus derivadas igual a 0) más una solución particular de la ecuación completa.
- Solución particular: Si fijando cualquier punto P(X0,Y0) por donde debe pasar necesariamente la solución de la ecuación diferencial, existe un único valor de C, y por lo tanto de la curva integral que satisface la ecuación, éste recibirá el nombre de solución particular de la ecuación en el punto P(X0,Y0), que recibe el nombre de condición inicial. Es un caso particular de la solución general, en donde la constante (o constantes) recibe un valor específico.
- Solución singular: una función que verifica la ecuación, pero que no se obtiene particularizando la solución general..




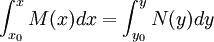





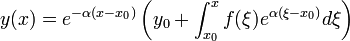


![y(x)={\frac {{e^{-\int \!P \left( x \right) {dx}}}}{\sqrt [\alpha-1]{ \left( 1-\alpha \right) \int \!Q \left( x \right) {e^{
\left( 1-\alpha \right) \int \!P \left( x \right) {dx}}}{dx}+C}}}](http://upload.wikimedia.org/math/9/a/4/9a47238d1aa4d74ae68a27dd1f66ea05.png)
![v(x) = [y(x)]^{(1-\alpha)}](http://upload.wikimedia.org/math/5/a/d/5ad96c3cb0277f5fd03823a426704314.png)



No hay comentarios:
Publicar un comentario